コレクション 角度 を 求める 259037-斜辺 から 角度 を 求める

エクセルで底辺と高さから角度を求める方法 まず、直角三角形における底辺、高さ、角度の関係を確認します。 角度にθ°を使用した場合、三角関数を用いて以下のような関係式が成り立ちます。 三角関数のtanθ＝高さ/底辺 で求めることができるため、 タンジェントの逆関数であるtan1 を使用するとθ＝tan1 （高さ/底辺）と計算できるのです。 エクセルでは、ATAN関数というものがこのtan1に 交点と原点の間に線を引き、 三角形の比 から角度を求める。 その際に、 θの範囲内にあるか 確認する という手順で三角関数の角度を求めることになります。 慣れてくればこの手順を意識しなくても自然と角度を求められるようになります。 最後にθの変域内にあるかを確認することが忘れられやすいので、きちんと条件を満たしていることを確認しましょう。 三角関数のグラフの書き よって，円の角度は何ラジアンかというと，円周の長さになるので，2π radになります． 度数法だと，円を360等分しているので，度数法と弧度法の関係は， 360° ＝ 2π rad になります． 2で割ると 180° ＝ π rad ですね． なんで弧度法が必要か！ ？ 弧度法というものがなぜ必要なのか，それは人々は楽をしたいからなのです． エレベータ万歳！ ！ 学校から帰るときは，歩くよ

サインから角度を計算するには Asin Degreesの解説 エクセル関数リファレンス

斜辺 から 角度 を 求める

斜辺 から 角度 を 求める-No 計算の内容 入力条件 計算 計算結果 1 水平距離・垂直距離 から勾配の計算 水平距離 と 垂直距離 勾配（％） 勾配（度） 一般に2通り求められます。 この場合，次の流れになります。 （a,b,Aがわかっているとします） 1 辺と対応する角が両方わかってる組 (a,A)を使い，正弦定理で外接円の半径Rを求める。 2 辺だけがわかっている組に正弦定理を使い，角度Bを求める。 3

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

対辺と隣辺の長さが分かっている時はtanを利用する この場合は、tan (x) = 対辺÷隣辺という公式を用います。 対辺が例えば75、さらに隣辺が100であるとしましょう。 75を100で割るので075となります。 つまり tan (x) = 075、あるいはx = tangent 1 (075)となります。 一覧表から値を探すか、計算機に075と入力しtangent1を押しましょう。 どちらの方法を用いても369度となるはずです。 角度 (θ)と距離が分かっている場合に座標Bを求める方法 θと距離から座標を求める処理 Copied!長さから角度計算 A＋B B＋C A＋C 三辺で長さが分かる物を2個、選び 下記にその数字を記入してください。 A B A

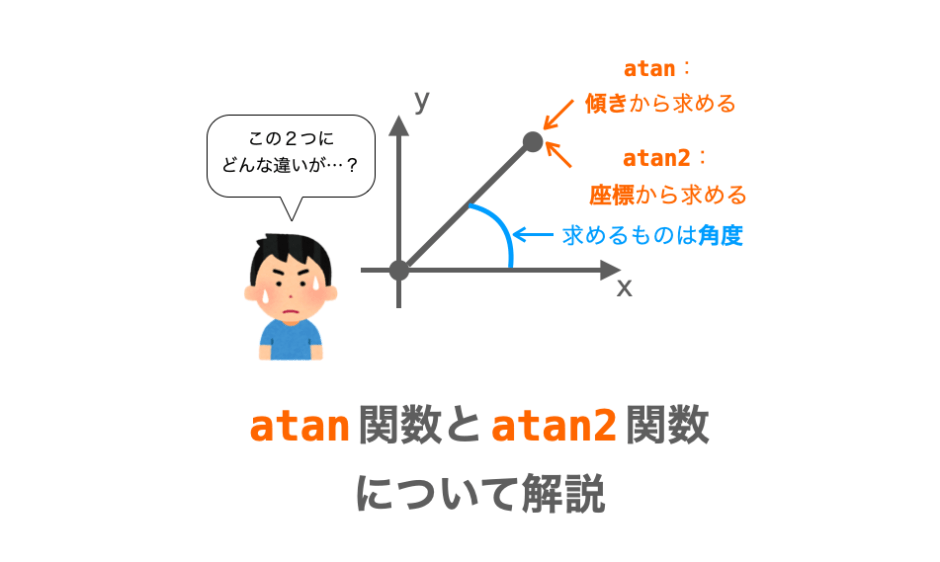
 したがって、角度が分かっている状態で直線の傾きを求めたいような場合に tan 関数が活躍します。 atan 関数 tan 関数とは逆に、atan 関数は「直線の傾き」から角度を求める関数です。 求められる角度の単位はラジアンです。角度から辺の比を求める問題も、2つの三角定規のどちらかを当てはめます。 すなわち、角度と1辺が分かっている場合は、他の辺の長さもわかることになります。 長方形、正方形の対角線の長さを求める 長方形や正方形と対角線の関係は、正に三平方の定理となります。 (対角線)² = 縦² ＋ 横² 従って、縦、横の長さが分かっていると、三平方の定理に当てはめて求めることができます。 直方体、立 角A、角Bの大きさを求めなさい。 解法 三角定規を組み合わせた問題はとてもよく出題されています。 わかる範囲で角度を図に記入してみましょう（右図の赤文字）。 三角定規では、 「 0°・60°・90° 」（右図水色）と 「 45°・45°・90° 」（右図黄色）の 三角形になることが大前提です。 それではまず、 角A からみていきます。 すると角Aは三角形 イ 、 ウ 、 エ の外角になってい

三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と斜辺) ・ 直角三角形 (底辺と角度) ・ 直角三角形 (高さと斜辺) ・ 直角三角形 (高さと角度) ・ 直角三角形 (斜辺と角度) ・ 角度から三角関数 ・ 三角関数から角度 (逆三角関数) ・ 三角関数の変換 このページのトップへ戻る/* θ (degree)にMathPI / 180を掛けているのはdegreeをradianに変換している radiusは半径である、距離とは半径を求めているのと同じ */ double radian = degree * MathPI / 180;勾配の高さ（高低差）をa、横の長さ（距離）をbとします。 角度の計算式を下記に示します。 θ（度）＝Atan (a/b)×180／π 上式を計算すれば角度が求められます。 詳細は下記が参考になります。 勾配の計算は？ 1分でわかる意味、単位、パーセント、1/100、パーセントの関係 屋根勾配3/100の角度 上表のとおり、屋根勾配3/100の角度は1718度です。 まとめ 今回は、勾配の角度表について説明

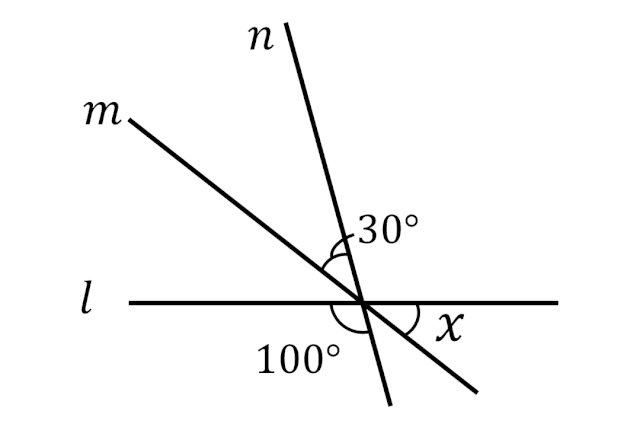
毎日脳トレ 図のxの角度はいくつ 中2レベル Dアプリ レビュー

三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

けっこう難問の角を求める問題 この問題は、現多良木中学校 毎床教頭から出していただき、私がちょっと悩んだ 問題です。 中学校の知識で解決できます。三角関数を利用して解決した先輩もいらっしゃ いましたが・・・三角形の角度を求める 問 ABC A B C について， BC B C の中点を D D とすると， ∠DAC = 15°，∠ADB = 45° ∠ D A C = 15 ° ， ∠ A D B = 45 ° となった． ∠BAD ∠ B A D を求めよ． 16/8/ 幾何 ★★★☆☆ hide or visible cはいきなり求めることができないので、dの角度を求めてから考えます。dはbと同位角の関係になるので、 d＝60° 直線の角の大きさは180°です。そのためcの角度は、180°60°＝1° よって、 答え a＝60°、b＝60°、c＝1° 例題3 下の四角形のaの角度を求めなさい。

Tikz 高校数学 三角比から角度を求める 数樂管理人のブログ

数学 中2 53 角度チャレンジ Lv 1 Youtube

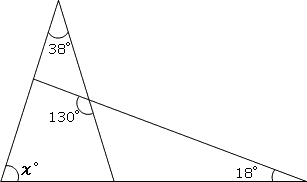
 土木業や建築業で仕事をしているとよく使われる「角度」「パーセント」「割合」。 頭の中がぐちゃぐちゃになりませんか？ 最近は換算してくれるサイトも増えてきましたが、いちいち入力するのは面倒ですよね。 そこで、私が普段から使っている換算表を公開します。 ただし、この表は私がエクセルで個人的に作成して個人的に使用しているものです。 これからご紹介する表の数値 角度を計算で求める方法をしっかりと理解するようにしていきましょう。 問題を見て 180度より大きい角か小さい 角かはすぐに分かるようにしましょう。 180度より小さい角は180度から引いてもとめることが多い 以下のような問題をまずは出来るようにしましょう。 あ の角度は ＝130° 180度より大きい角は360度（1周分）から180度より小さい角を引いて求めることが多い三角関数の角度を計算する場合、「エクセル」を使うと便利です。 θ＝Arcsin (038)のような半端な辺の比に対する角度も計算できます。 まずエクセルのセルに「= ASIN (038)」と入力してください。 結果はラジアンで出力されるので「×180/314」で度数表示できます。 ※ちなみにASIN (038)＝22°程度です。 ラジアンの詳細は下記をご覧ください。 弧度とは？ 1分でわかる意味、読み方、ラジアン

小５ 算数 小５ ３１ 三角形の角 Youtube

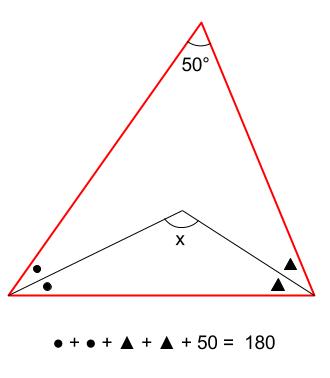
中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su

このページには 01° 単位の三角関数表を掲載しています。角度に対するサイン、コサイン、タンジェント、およびラジアンの値を知りたいときに、ご利用ください。 また、表の後では、三角関数の定義と、周期性・対称性による変換公式を紹介しています。 この角度θをエクセルで求める方法です。 実際にマーケティングの分野でも角度を求めることができれば、 原点からの距離と角度で順位付けできたりする ので、便利になりますよ！ 実際に、座標からの角度計算を活用するマーケティング関連記事もチェック！ 角度によっては、こんなふうに直線じゃなくなっちゃうよね。 だから、bd´ が直線であることを証明する必要があるよ。 これを証明するには、もう一つ三角形を付け足すんだ。 こんな感じ

３点の座標から簡単に角度と回転方向を求める 2 3 N次元 外積を用いる方法

角度の計算 裏技まとめ 教遊者

 角度は、次の2段階のステップで求めます。 求める角度の余弦（cos (コサイン)）を求める。 余弦から角度を求める。 第1ステップで余弦定理を使います。 余弦定理の公式を覚えていればそれに当てはめるだけで余弦が求まります。 辺から余弦 (コサイン)を求める 第二余弦定理を変形した公式を使えば、辺の長さから余弦を求めることができます。 第二余弦定理の使用例 辺の長さが、今、ノートパソコン、コンピュータ、タブレット、またはスマートフォンを使って、いつでもどこでも、私たちの周りのものの角度を測定することができます。 小さいものを測定したい場合は、それを画面に配置して測定してください。 もっと大きいものを測定したい場合は、写真を撮ってそれをアップロードしてから、分度器の中心点を動かして角度を測定します。 カメラまたは画像を使用しこの表し方を極形式と言います。 積の複素数の偏角は、偏角の和になります（→※）： a r g ( w z) = a r g w a r g z 商の複素数の偏角は、偏角の差になります（→※）： a r g ( w z) = a r g w − a r g z ※このページでは、偏角 θ は 0 ≤ θ < 2 π を満たすような

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

三角形の角度を求める問題 小学生 中学生の勉強

 この記事では、三角関数について、角度の求め方や変換公式（\\(90^\\circ − \\theta\\) など）について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターしてくださいね！ まずは、「2辺の長さとその間の角度」から「残り1辺の長さ」を求める場合。 b = A C = 4 c = A B = 6 cos A = cos 60 ° = 1 2 を代入すると、残り1辺の長さ a が求まります。 3辺の長さ⇒角度 次に、3辺の長さから角度を求める場合。 この場合は、余弦定理の式を「 cos A = ⋯ 」の形に式変形してから a, b, c を代入すると cos A = 1 2 と求まり、 A の内角が 45 ° であることが分かります 角度 (°) ＝ arctan (勾配) × 360 ÷ π で計算することができる。 距離の計算 三平方の定理より 斜辺 2 ＝ 水平距離 2 ＋ 高さ 2 で求められる。 角度と勾配 (％)の換算 角度と％の換算は 角度→勾配 (％) 勾配 (％) ＝ sin (角度) × 100 勾配 (％)→角度 角度 (°) ＝ arctan (勾配) × 360 ÷ π で求めた。

Math 中学受験の難問 角度を求める問題 働きアリ

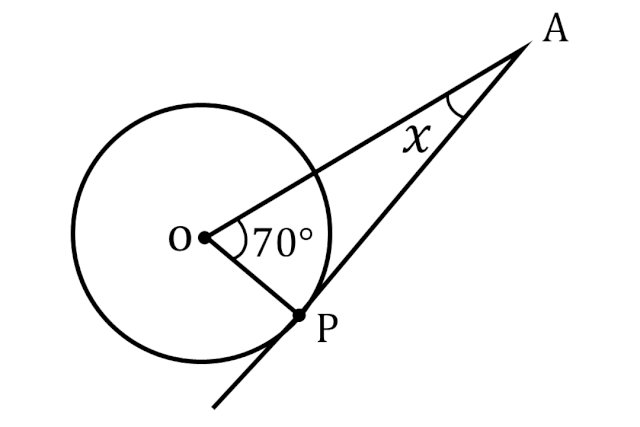
毎日脳トレ なんとなくじゃダメ Xの角度は 中1レベル Dアプリ レビュー

 二つのベクトルがつくる角度を0～360度の範囲で求めたい。 内積関数に2つのベクトルを渡し、 返ってきた値を、アークコサイン関数に渡す。 そうすると角度が返ってくる。 このやり方で求めることが出来るのは、 右回り、左回り0～180度の範囲。 ってことは、「比例式から求める方法」を知っておけば公式を忘れても大丈夫ってことになる。 念のために、 公式に頼らない「扇形の中心角の求め方」 をみていこう。 さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。斜面（勾配）の角度は、三角形の斜辺と高さが分かれば計算できます。 又は斜辺と底辺が既知でも良いです。 角度θを求める計算式はθ＝Atan (a/b)です。 また、角度の値が既知であれば斜辺、高さ、底辺の長さを計算できます。 今回は、角度の計算と斜辺、高さの関係、辺の長さから角度を求める方法について説明します。 傾斜、勾配の計算については下記が参考になります。 傾斜の計算とは？ 1

正弦定理 角度を求める 一夜漬け高校数学1 Youtube

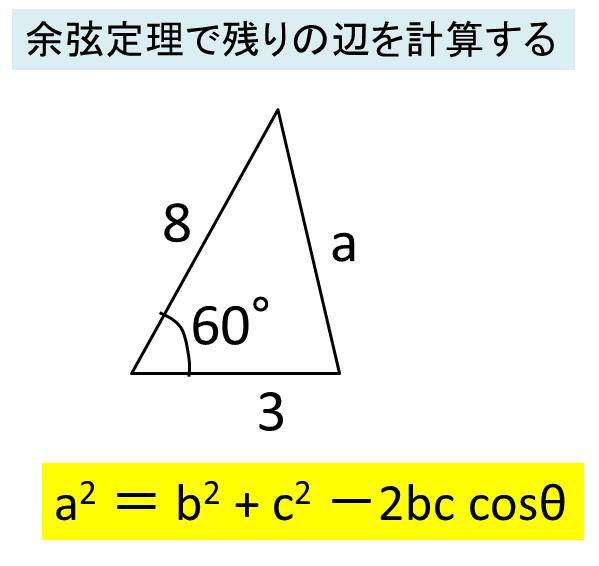
Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める

底辺と高さから角度と斜辺を計算 高精度計算サイト 底辺と高さから角度と斜辺を計算 ホーム / 数学公式集 / 三角関数（度） 答えの度分秒（° ′ ″ ）は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c , sinθ= b c , tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e ( 1) cos θ = a c , sin θ = b c , tan θ = b a ( 2) P y t h a g o r e a n t h e o r e m a 2 b 2 = c 2 お

底辺と高さから角度と斜辺を計算 高精度計算サイト

Unity 2つのベクトル間の角度を求める ねこじゃらシティ

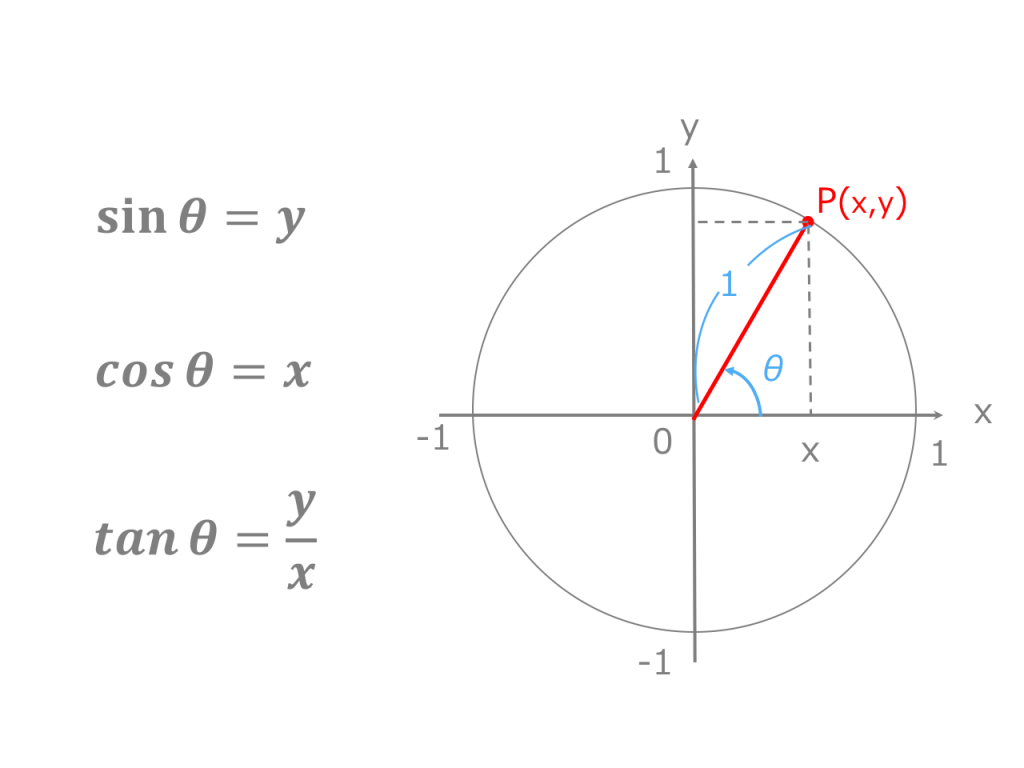
3分で分かる 三角方程式の解き方 単位円を用いた三角関数の角度の求め方 をわかりやすく 合格サプリ

中学数学の問題 図形 角度を求める

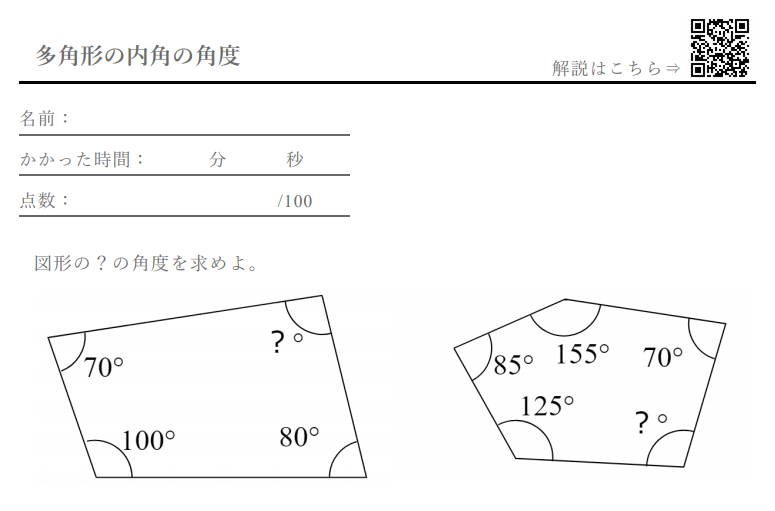
多角形 の内角の角度 計算ドリル 問題集 数学fun

サインから角度を計算するには Asin Degreesの解説 エクセル関数リファレンス

C言語 Atan関数とatan2関数について解説 傾きor座標から角度を求める関数 だえうホームページ

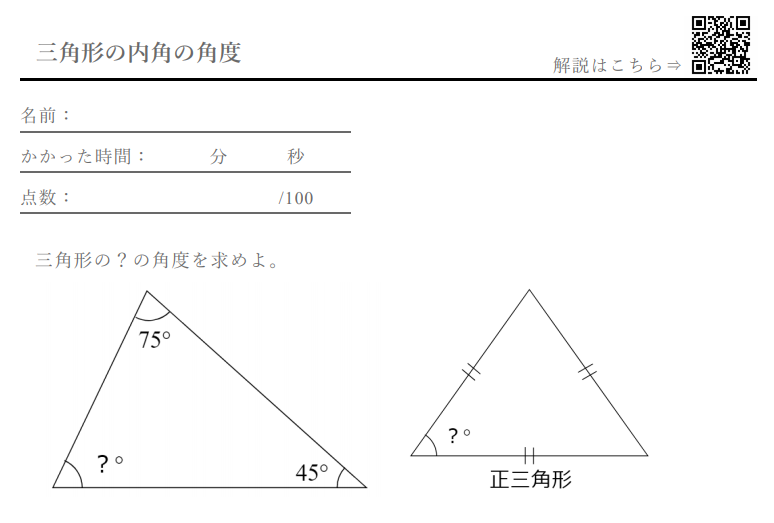
三角形 の内角の角度 計算ドリル 問題集 数学fun

中学受験 平面図形 重なった正方形と正三角形から角度を求めるには さんすうがく

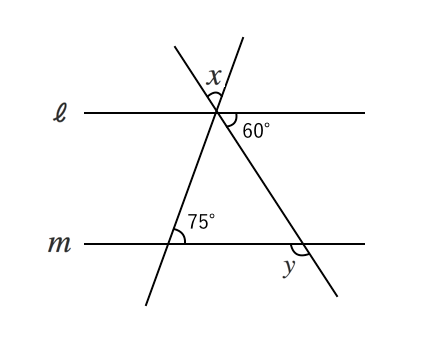
図形の調べ方 角度を求める問題 苦手な数学を簡単に

中2数学 ブーメラン型角度の求め方を解説 数スタ

二等辺三角形の角度 無料で使える中学学習プリント

三角形の辺から角度を計算 製品設計知識

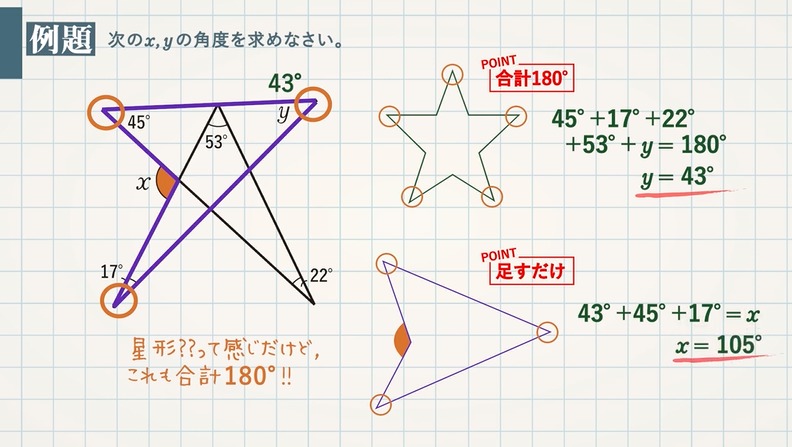
角度の計算 裏技まとめ 教遊者

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

角度の求め方 算数の教え上手 学びの場 Com

２つのベクトルのなす角度を求める

Java ２つのベクトルがなす角度を求める Shogonir Blog

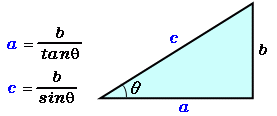
角度と高さから底辺と斜辺を計算 高精度計算サイト

角度の計算と斜辺 高さの関係は 3分でわかる計算 求め方 辺の長さから角度を求める

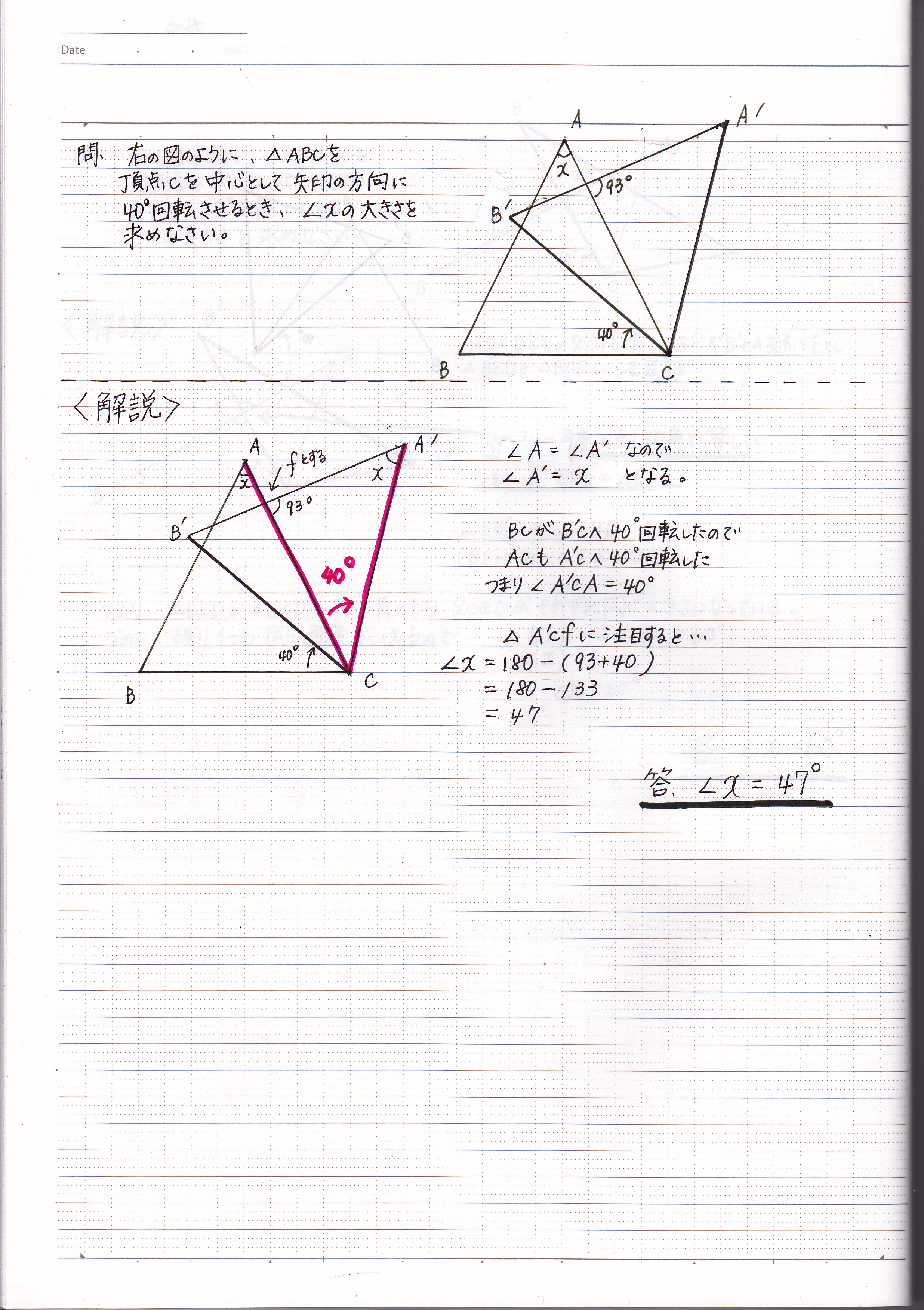
回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

エクセルで座標から角度を求める方法 しおビル ビジネス

の角度を計算でどうやって求めるんですか の角度を計算でどうやっ 計算機科学 教えて Goo

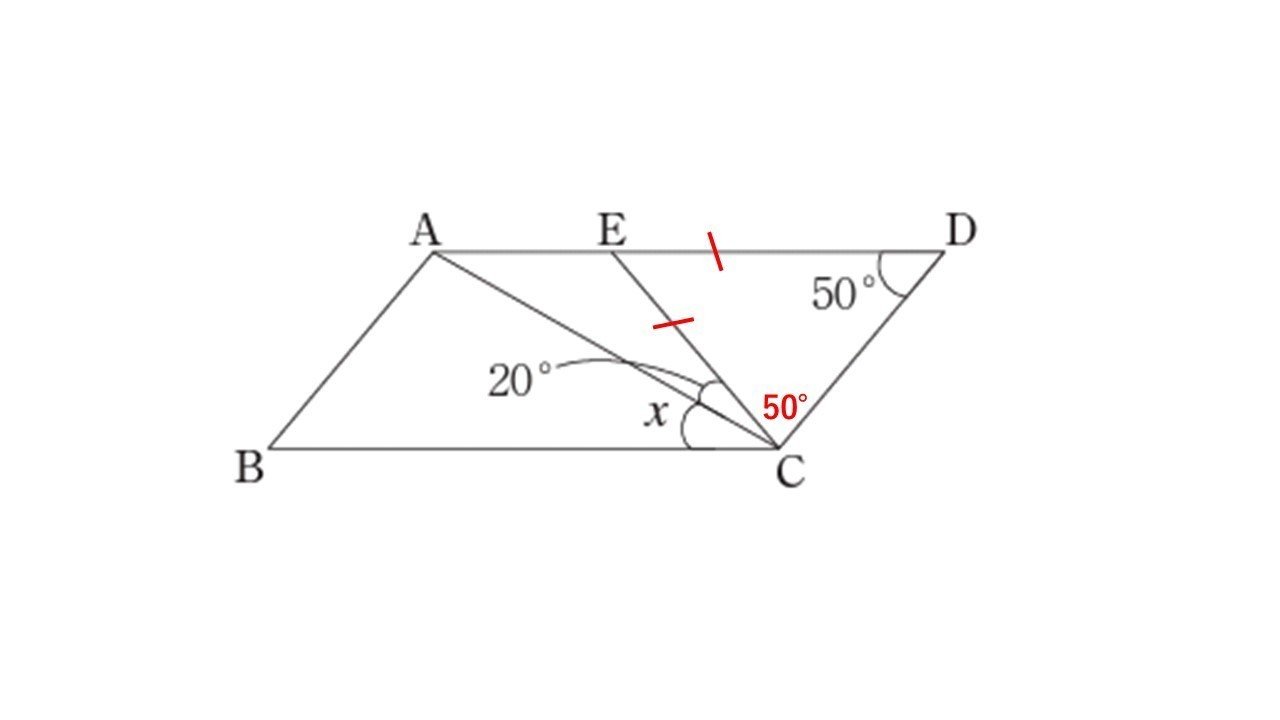
中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学 Note

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に

Pythonで座標データから角度を求める方法 アークコサインを使った方法 文系駆け出しでどこまでプログラム上達できるのか 成長のための備忘録ブログ

三角形の角度を求める問題 小学生 中学生の勉強

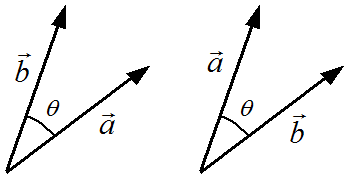
３点からなる角度を求める 画像処理ソリューション

面白い数学の問題 角度を計算しよう 小学生の問題集より そらの暇つぶしch

いろいろな角度を求める問題２ 折り曲げ 中学受験準備のための学習ドリル

角度の簡易計算

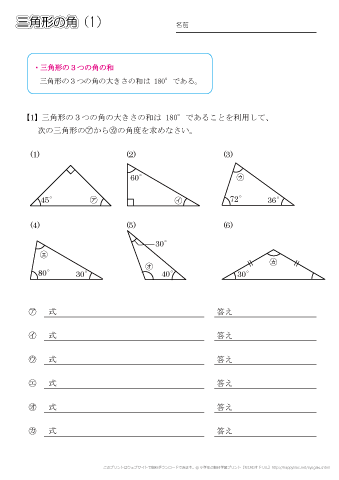
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

平面図形 円の中にある三角形の角度を求めるには 早稲田中学校の入試問題から 親子で挑戦 中学受験算数 朝日新聞edua

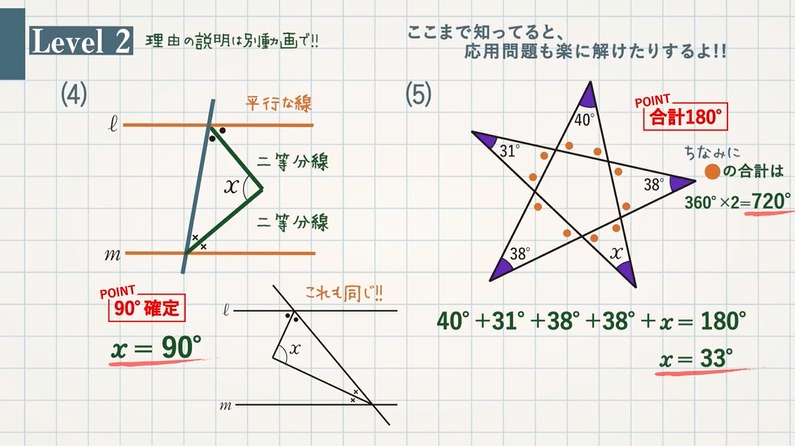
角度の計算 裏技まとめ 教遊者

小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

三角形の角度を求める問題 小学生 中学生の勉強

図形の角度を求める応用問題２ 数学総復習

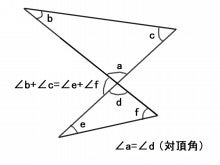
角度の求め方 数学が嫌いなんです

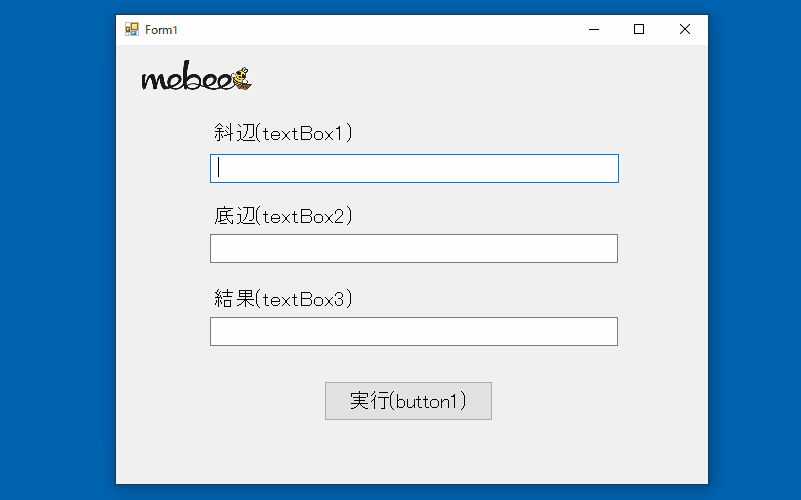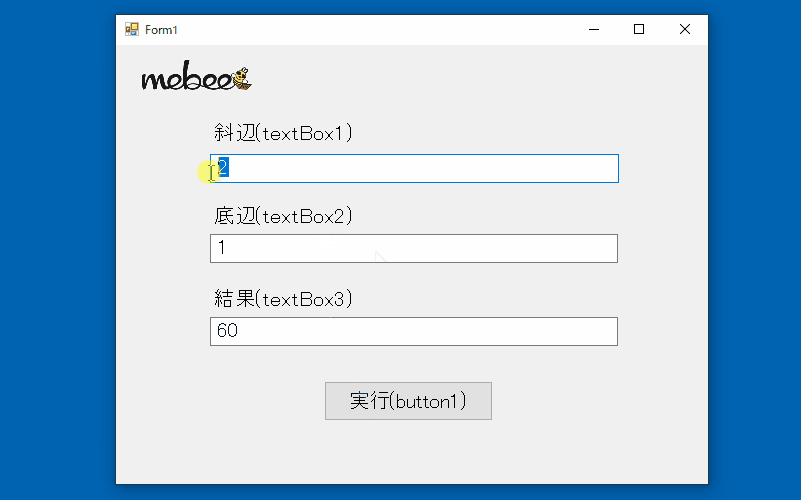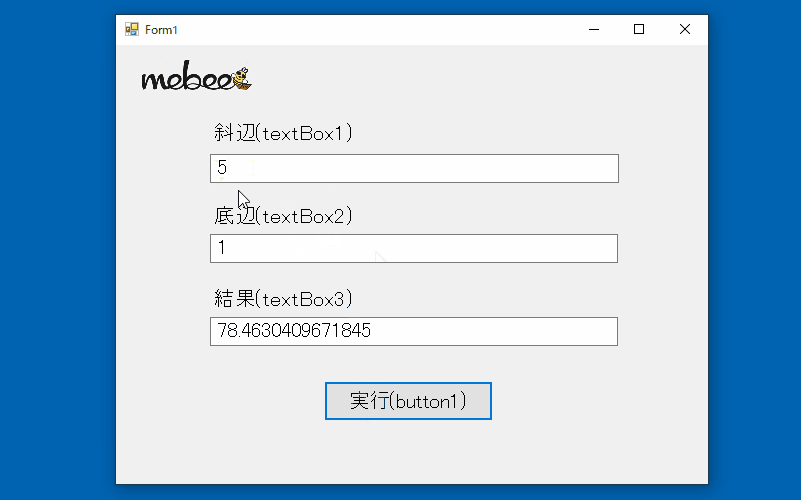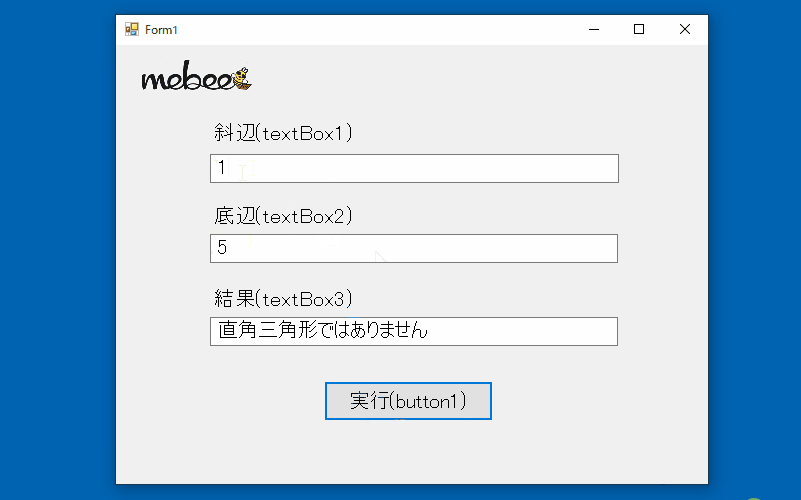
C Acosメソッドを使用して直角三角形の角度を求める Mebee

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

いろいろな角度を求める問題３ 平行線や三角形の性質 中学受験準備のための学習ドリル

3

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

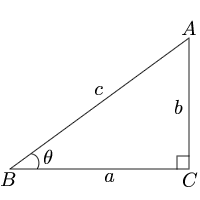
三角関数から角度 逆三角関数 三角形の計算 計算サイト

簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage

ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく

高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット

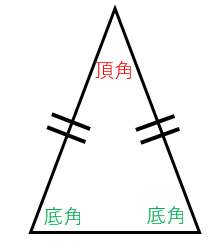
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学

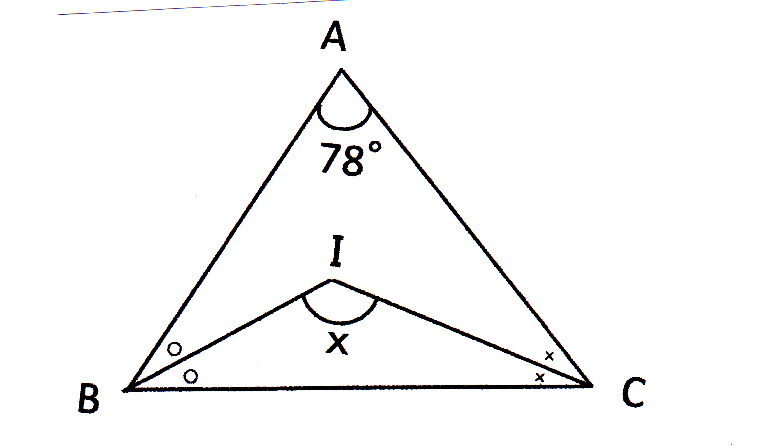
三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方

三角形の角度を求める 思考力を鍛える数学

1

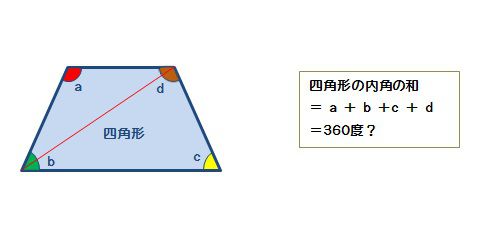
四角形の内角の和 算数の公式覚えてますか

余弦定理で角度を求める方法 数学の星

小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ

角度の求め方 算数の教え上手 学びの場 Com

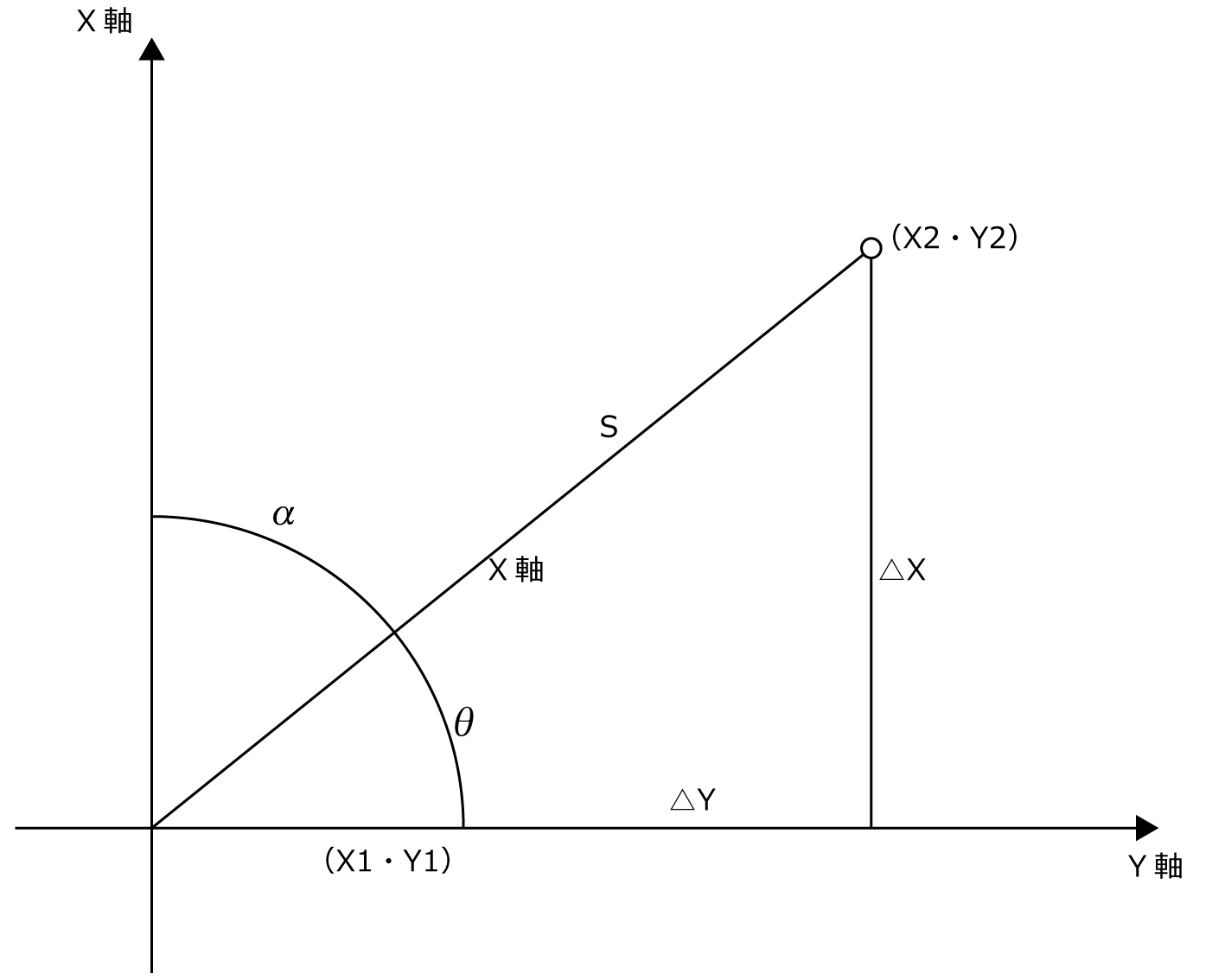
座標から角度の求め方 測量 測量機の情報ページ

台形とは 定義や 台形の面積の公式をわかりやすく解説 受験辞典

ラングレーの問題 整角四角形

二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思う Clearnote

高校数学 三角比からの角度の求め方3 Tan8 練習編 映像授業のtry It トライイット

二等辺三角形の角を求める Youtube

角度の求め方 算数の教え上手 学びの場 Com

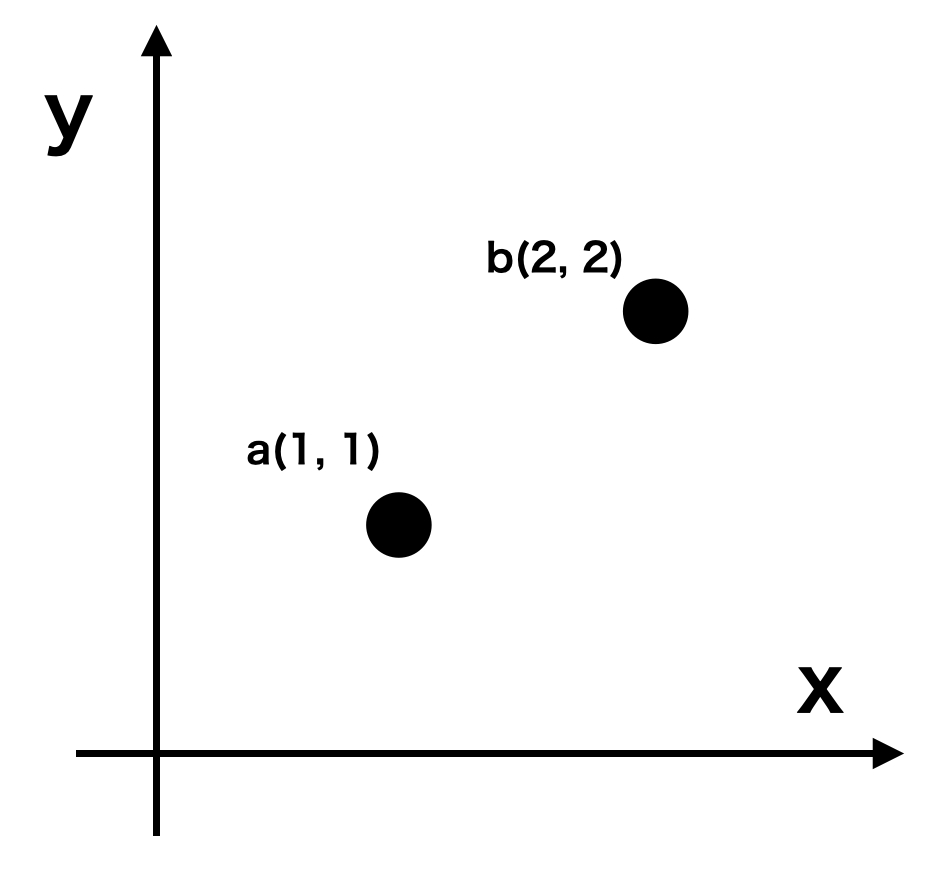
Python Numpyで2点間の距離と角度を求める Kaggle Note

底辺と角度から 高さを求める ある高さの木から 10m離れて 木のてっ Okwave

中学受験 平面図形 重なった２つの三角形から角度を求めるには さんすうがく

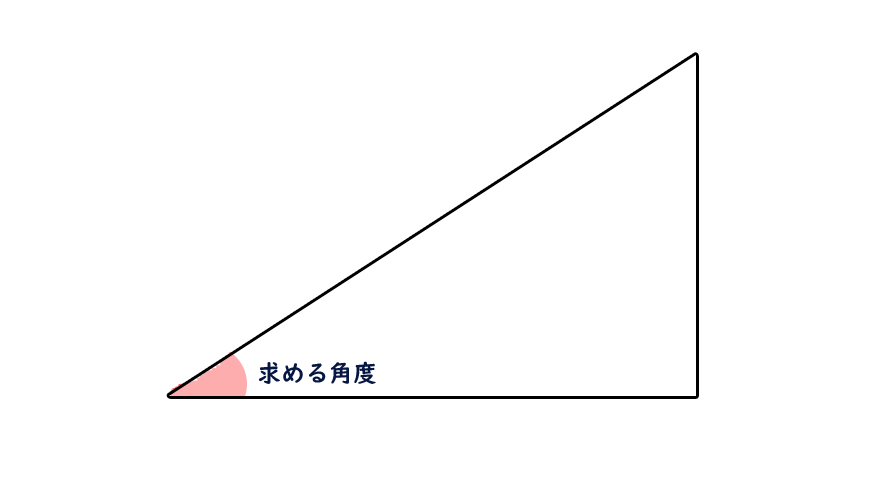
C Atanメソッドを使用して直角三角形の角度を求める Mebee

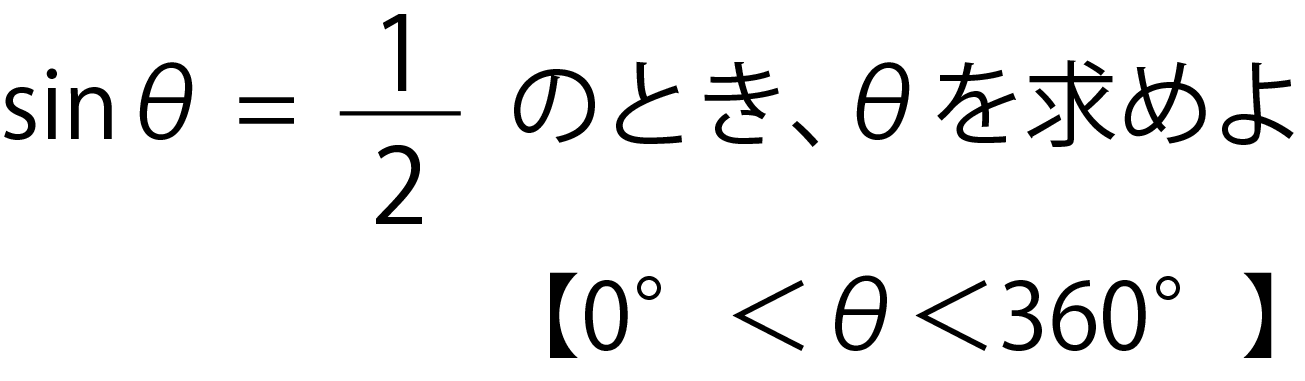
三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

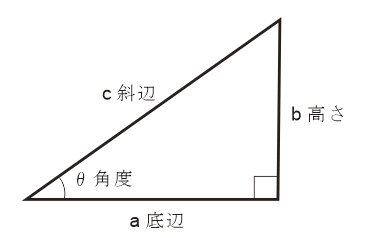
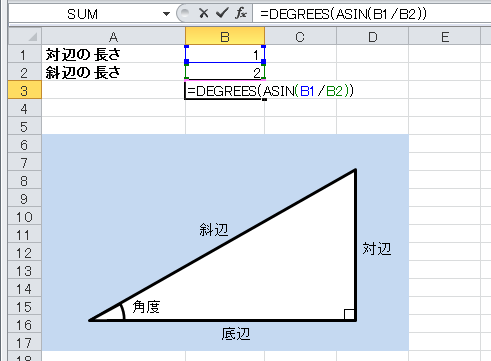
表計算ソフトを使って 底辺 と 高さ から 角度 を求める

中2数学の角度の求め方について質問です 25 以外全く角度がわかりませんど Yahoo 知恵袋

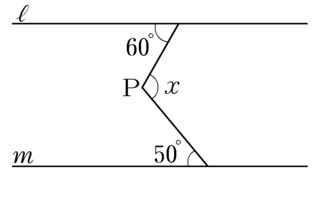
角度を求める 補助線 Takapの数学日記

Unity 2つのベクトル間の角度を求める ねこじゃらシティ

勉強しよう数学解答集 余弦定理を使って角度を求める解答

外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題

三角形の角度を求める問題がわかりません 三角形の和と直線の角度 Yahoo 知恵袋

正確な角度の測定 割り付け

実際大学入試も角度を求めるときに記述しますか Clearnote

角を求める問題

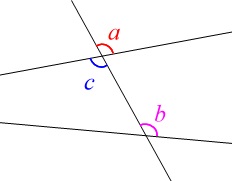
平行線の同位角と錯角を利用して角度を求める問題の解き方

中学受験 平面図形 折り返した長方形の中の角度を求めるには さんすうがく

1

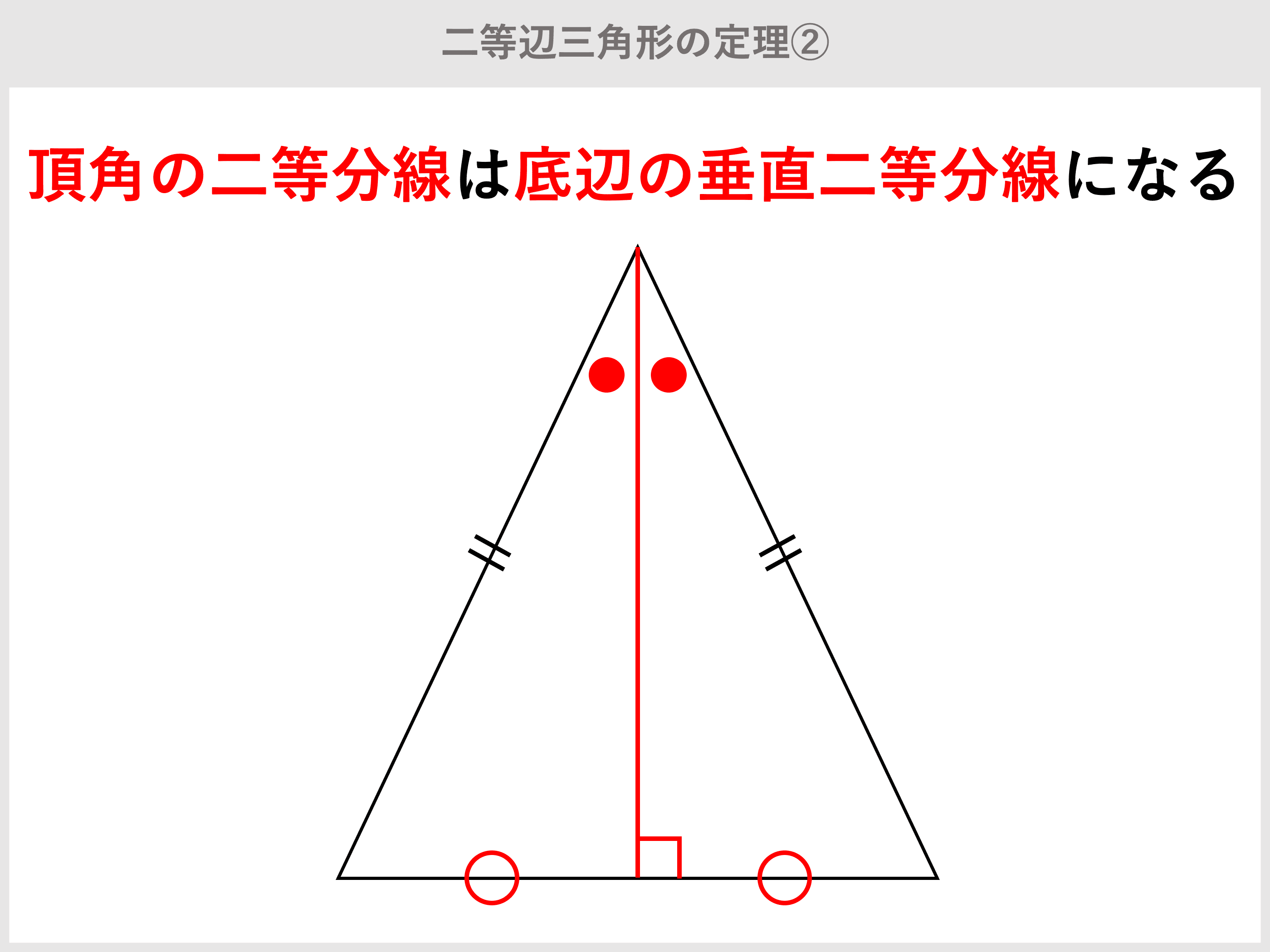
三角角度求め方 Motics

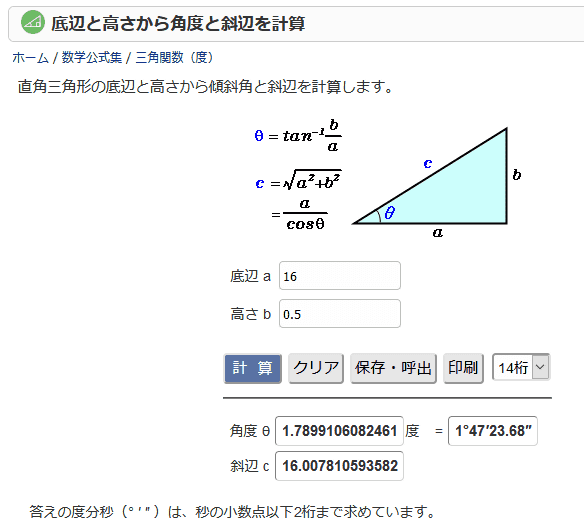
表計算ソフトを使って 底辺 と 高さ から 角度 を求める

角度を求める問題 中学受験 田中貴 Com

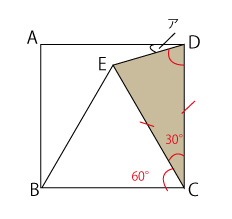
いろいろな角度を求める問題1 図形の等辺を利用する 中学受験準備のための学習ドリル

1

コマネチ大学数学科94講 謎の難問 ガスコン研究所

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す

Incoming Term: 角度 を 求める 難しい 問題, 斜辺 から 角度 を 求める,